Here’s the situation:

I have a little sister in 6th grade. One day, she got stuck on a problem from a certain online math program (which I won’t name here). My dad went over to help her, but the problem ended up stumping him as well. I went over to take a look, and was greeted by this:

Find the value of x that makes the expressions equivalent.

4(x-5); 32-20

We all sat and stared at the problem for a minute or so. Even with an adult high-school graduate on the left and an AP Calculus student on the right, a 6th-grade math problem left all of us confused. A semicolon? What does that mean? Then I realized, “Oh, they’re basically saying this:”

Solve for x.

4(x-5) = 32-20

Okay, I get that it sounds like I’m nitpicking here. After all, it’s a very easy problem once you realize what it’s asking for.

But it takes effort to make that realization in the first place, and that’s what I don’t understand. Why would the problem be written in such a wordy, obtuse manner? After all, this is being given to 6th graders. Shouldn’t the instructions be as clear and simple as possible? When comparing their version of the problem to mine, the actual meat of the problem (a test of algebra) remains unchanged. In that case, why not explain the problem with half the words?

It’s also not a stretch to see why this problem confused my father and I. In fact, if you have kids or siblings, you’ve probably had a similar experience. It’s common to overthink an easy problem when it’s presented in an unfamiliar way. I’ve done tens of thousands of algebra problems with this setup: here’s an equation; solve for x. This routine process is one of the fundamental staples of any math curriculum involving algebra. It presents a consistent framework and setup, allowing students to focus on the actual skills they’re trying to learn and practice. So wouldn’t it be ideal to get kids acquainted with this tried-and-true format, one that will be with them for—hey John, check it out! Look how fancy we sound if we use semicolons!

And it’s not just a problem at the elementary level. This experience reminded me of last summer when I volunteered as a math tutor for summer school at Pinole Middle. Whenever a student asked me for help, the reason was almost always because they just didn’t understand the instructions. Once I had the problem deciphered, they could usually handle the rest on their own. I felt more like a translator than a math tutor.

No wonder math gets such an infamous reputation. But does it have to be that way?

(I suppose it might sound a bit arrogant to make suggestions on how prestigious math majors should do their jobs, but hey, I am someone who’s going through this whole curriculum thing. )

—

If you think about it, math is a language. Languages, in a broad sense, are methods of communication that use defined signals to represent various things. “Tree.” You just pictured something with leaves and branches, right? That’s because you understand what the signal represents, and therefore you can tell what I’m trying to communicate. If you don’t read English, then first off, how did you get this far? But more importantly, you probably haven’t learned what the word “tree” represents. You’d just see four symbols that lack any significance.

So how is math a language? Well, take a look at this symbol: + . This symbol is a signal which represents the operation of addition, communicating that two things are being combined. See the connection? If you don’t know basic math, then a plus symbol merely looks like a cross, nothing more. If you do know basic math, then when I use that symbol in a “sentence” (read: equation), say, 1 + 1 = x, you’ll quickly work out that x=2.

Are you with me so far? Good, because I’m about to go on another tangent (trust me, this all leads somewhere).

Computer code, from HTML to JavaScript to Python, is a form of language that’s all about issuing commands and orders. However, it stands out because of one key factor: the audience is a machine. This is a very double-edged sword. On one hand, a computer will be able to instantly memorize and perfectly execute any order within its capabilities. On the other hand, you must be extremely precise in issuing out those orders. Artificial intelligence lacks the human flexibility of seeing past minor language errors. I’ve worked with programming in our school’s Engineering Academy, and I will testify that a single misplaced punctuation mark can make a robot go braindead.

Humans are like the polar opposite of computers, at least when it comes to learning. We can’t instantly learn things as computers do, and we’re prone to making errors in our execution. But we have a much better sense of judgement and flexibility, especially when language is concerned. Some people pronounce “caramel” with three syllables, while others pronounce it with two. It’s never stopped us from understanding what someone else is saying. We argue about it anyways, but the follies of mankind are besides the point.

Now here’s where everything comes together.

Remember those examples of overly-complicated math instructions? Those are perfect examples of trying to teach humans as if they are machines. Yes, they may be technically correct, but at some point they become less useful due to the amount of jargon involved. Keep in mind that we frequently use words such as “ain’t,” even though they are considered to be improper English. We have to ask ourselves: what is more important? How we say something? Or that we understand what we’re saying?

—

The great Mr. Mazaheri, bless his soul, once gave us a lecture on the Pythagorean Theorem. You may recognize this as the equation, “a squared plus b squared equals c squared.” He didn’t care much for this formula because of its ambiguity. Which side is “a”? What about “b” or “c”? It was too vague to work as a definition.

What he proposed instead, was to memorize its correct definition: “The square of the hypotenuse of a right triangle is equal to the sum of the squares of the other two sides.”

OK, I had to Google that. But it goes to show that, while this definition might be more technically correct, it’s not as immediately helpful for learning what the theorem is really trying to say. It’s very wordy, and you have to know what a hypotenuse is. Compare it to this:

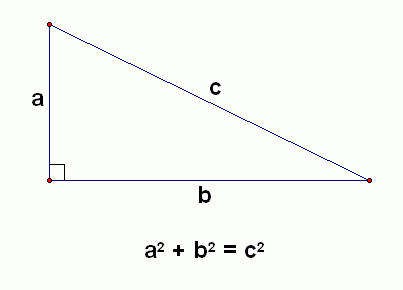
That’s much better, right? All it takes is a simple visual to learn this theorem’s meaning. And yes, you could argue that I could “fool” someone by switching around the places of the letters. But if I’m a teacher, why would I be interested in doing that? If this example is consistently shown to students enough times, they’ll start picking up on patterns: they’ll realize that “a” and “b” are always at a right angle to each other (or at least that they both touch the little square thing in the corner). Why? Because they’re human, and that’s just how the human learning process works.

—

This article has taken me a while to finish, and I’ve rambled so much that I’ve forgotten about 94% of what I’m even trying to say.

And of course, take everything I say with a grain of salt. It’s definitely important for students to learn what a hypotenuse is, and precise instructions can sometimes be necessary for standardized tests and the like. But it’s a fact that math is often one of the hardest subjects for students to learn, and I believe we can change that. Perhaps if we rethink the way math is taught, we’ll learn a lot more than just 6th grade algebra.